
Depois de traduzir algumas das equações complicadas da matemática, os pesquisadores criaram um sistema de inteligência artificial que eles esperam responder a perguntas ainda maiores.
Mais de 70 anos atrás, pesquisadores na vanguarda da pesquisa em inteligência artificial introduziram redes neurais como uma maneira revolucionária de pensar sobre como o cérebro funciona. No cérebro humano, redes de bilhões de neurônios conectados fazem sentido dos dados sensoriais, permitindo-nos aprender com a experiência. As redes neurais artificiais também podem filtrar grandes quantidades de dados através de camadas conectadas para fazer previsões e reconhecer padrões, seguindo regras que eles mesmos aprenderam.
Até agora, as pessoas tratam as redes neurais como um tipo de panacéia de IA, capaz de resolver desafios tecnológicos que podem ser reapresentados como um problema de reconhecimento de padrões. Eles fornecem tradução de idioma com som natural. Os aplicativos de fotos os usam para reconhecer e categorizar rostos recorrentes em sua coleção. E programas conduzidos por redes neurais derrotaram os melhores jogadores do mundo em jogos como Go e xadrez.
No entanto, as redes neurais sempre ficaram para trás em uma área visível: resolver problemas matemáticos simbólicos difíceis. Isso inclui as características dos cursos de cálculo, como integrais ou equações diferenciais ordinárias. Os obstáculos surgem da própria natureza da matemática, que exige soluções precisas. As redes neurais tendem a se sobressair na probabilidade. Eles aprendem a reconhecer padrões – qual tradução soa melhor ou como é o seu rosto – e, a partir daí, podem gerar novos.
A situação mudou no final do ano passado, quando Guillaume Lample e François Charton, um par de cientistas da computação que trabalhavam no grupo de pesquisa de IA do Facebook em Paris, revelaram uma primeira abordagem bem-sucedida para resolver problemas matemáticos simbólicos com redes neurais. O método deles não envolve trituração de números ou aproximações numéricas. Em vez disso, eles jogaram com os pontos fortes das redes neurais, reformulando os problemas de matemática em termos de um problema praticamente resolvido: tradução de idiomas.
“Nós dois nos formamos em matemática e estatística”, disse Charton, que estuda aplicações da IA na matemática. “Matemática era a nossa língua original.”
Como resultado, o programa de Lample e Charton poderia produzir soluções precisas para integrais complicadas e equações diferenciais – incluindo algumas que surpreendiam pacotes populares de software de matemática com regras explícitas de solução de problemas incorporadas.
O novo programa explora uma das principais vantagens das redes neurais: elas desenvolvem suas próprias regras implícitas. Como resultado, “não há separação entre as regras e as exceções”, disse Jay McClelland, psicólogo da Universidade de Stanford que usa redes neurais para modelar como as pessoas aprendem matemática. Na prática, isso significa que o programa não tropeçou nas integrais mais difíceis. Em teoria, esse tipo de abordagem poderia derivar “regras” não convencionais que poderiam avançar em problemas que atualmente são insolúveis por uma pessoa ou uma máquina – problemas matemáticos como descobrir novas provas ou entender a natureza das próprias redes neurais.
Não que isso tenha acontecido ainda, é claro. Mas está claro que a equipe respondeu à pergunta de décadas atrás – a IA pode fazer matemática simbólica? – afirmativamente. ?Seus modelos estão bem estabelecidos. Os algoritmos estão bem estabelecidos. Eles postulam o problema de maneira inteligente ?, disse Wojciech Zaremba, co-fundador do grupo de pesquisa de IA OpenAI.
“Eles conseguiram criar redes neurais que pudessem resolver problemas que estavam além do escopo do sistema de máquinas que seguem regras”, disse McClelland. “O que é muito emocionante.”
Ensinar um computador a falar matemática
Os computadores sempre foram bons em analisar números. Os sistemas de álgebra computacional combinam dezenas ou centenas de algoritmos conectados com instruções predefinidas. Eles geralmente são seguidores de regras estritos, projetados para executar uma operação específica, mas incapazes de acomodar exceções. Para muitos problemas simbólicos, eles produzem soluções numéricas suficientemente próximas para aplicações de engenharia e física.
Redes neurais são diferentes. Eles não têm regras rígidas. Em vez disso, eles treinam em grandes conjuntos de dados – quanto maior, melhor – e usam estatísticas para fazer aproximações muito boas. No processo, eles aprendem o que produz os melhores resultados. Os programas de tradução de idiomas brilham particularmente: em vez de traduzir palavra por palavra, eles traduzem frases no contexto de todo o texto. Os pesquisadores do Facebook viram isso como uma vantagem para resolver problemas matemáticos simbólicos, não um obstáculo. Dá ao programa uma espécie de liberdade de resolução de problemas.
Essa liberdade é especialmente útil para certos problemas em aberto, como a integração. Há um velho ditado entre matemáticos: “Diferenciação é mecânica; integração é arte.” Isso significa que, para encontrar a derivada de uma função, você só precisa seguir alguns passos bem definidos. Mas encontrar uma integral geralmente requer outra coisa, algo mais próximo da intuição do que do cálculo.
O grupo do Facebook suspeitou que essa intuição pudesse ser aproximada usando o reconhecimento de padrões. “A integração é um dos problemas mais semelhantes ao reconhecimento de padrões em matemática”, disse Charton. Portanto, mesmo que a rede neural possa não entender o que as funções fazem ou o que as variáveis significam, elas desenvolvem um tipo de instinto. A rede neural começa a sentir o que funciona, mesmo sem saber o porquê.
Por exemplo, um matemático solicitado a integrar uma expressão como yy'(y2 + 1)?1/2 suspeitará intuitivamente que o primitivo – ou seja, a expressão que foi diferenciada para dar origem à integral – contém algo que se parece com o raiz quadrada de y² + 1.
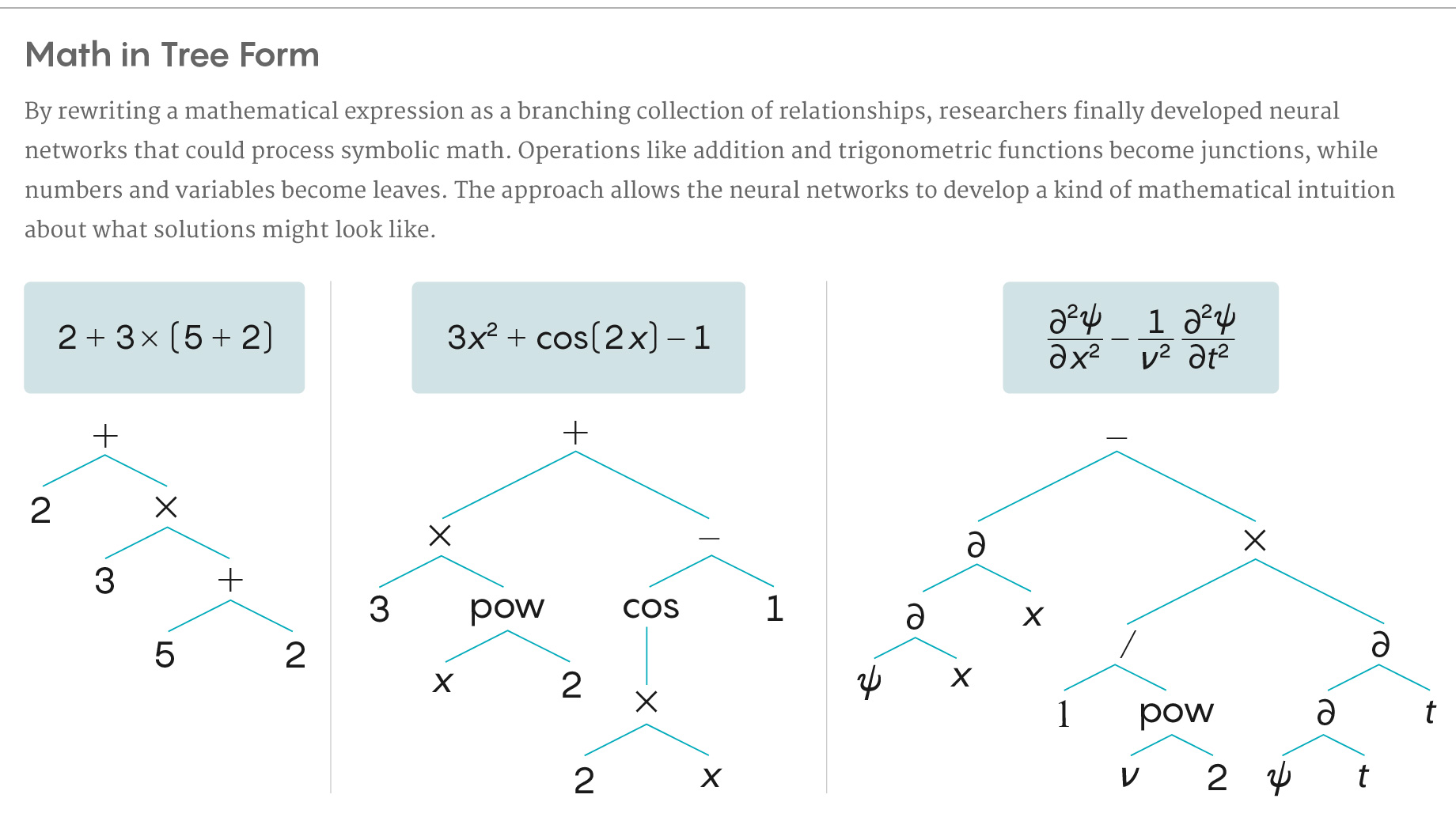
Para permitir que uma rede neural processasse os símbolos como um matemático, Charton e Lample começaram traduzindo expressões matemáticas em formas mais úteis. Eles acabaram reinterpretando-os como árvores – um formato semelhante em espírito a uma frase diagramada. Operadores matemáticos como adição, subtração, multiplicação e divisão tornaram-se junções na árvore. O mesmo aconteceu com operações como aumentar a potência ou funções trigonométricas. Os argumentos (variáveis e números) se tornaram folhas. A estrutura em árvore, com muito poucas exceções, capturou a maneira como as operações podem ser aninhadas em expressões mais longas.
“Quando vemos uma função grande, podemos ver que ela é composta de funções menores e tem alguma intuição sobre qual pode ser a solução”, disse Lample. “Achamos que o modelo tenta encontrar pistas nos símbolos sobre qual pode ser a solução.” Ele disse que esse processo é paralelo ao modo como as pessoas resolvem integrais – e realmente todos os problemas de matemática – reduzindo-os a subproblemas reconhecíveis que já haviam resolvido antes.
Após criar essa arquitetura, os pesquisadores usaram um banco de funções elementares para gerar vários conjuntos de dados de treinamento, totalizando cerca de 200 milhões de equações e soluções (em forma de árvore). Eles então “alimentaram” esses dados à rede neural, para que pudessem aprender como são as soluções para esses problemas.
Após o treinamento, chegou a hora de ver o que a rede poderia fazer. Os cientistas da computação testaram 5.000 equações, desta vez sem as respostas. (Nenhum desses problemas de teste foi classificado como “insolúvel”.) A rede neural passou com cores vivas: conseguiu obter as soluções certas – precisão e tudo – para a grande maioria dos problemas. Ele se destacou particularmente na integração, resolvendo quase 100% dos problemas de teste, mas teve um pouco menos sucesso nas equações diferenciais comuns.
Para quase todos os problemas, o programa levou menos de 1 segundo para gerar soluções corretas. E nos problemas de integração, ele superou alguns solucionadores nos populares pacotes de software Mathematica e Matlab em termos de velocidade e precisão. A equipe do Facebook informou que a rede neural produzia soluções para problemas que nenhum desses solucionadores comerciais poderia resolver.
Na caixa preta
Apesar dos resultados, o matemático Roger Germundsson, chefe de pesquisa e desenvolvimento da Wolfram, fabricante da Mathematica, discordou da comparação direta. Os pesquisadores do Facebook compararam seu método a apenas algumas das funções do Mathematica – “integrar” para integrais e “DSolve” para equações diferenciais – mas os usuários do Mathematica podem acessar centenas de outras ferramentas de solução.
Germundsson também observou que, apesar do tamanho enorme do conjunto de dados de treinamento, ele incluía apenas equações com uma variável e apenas aquelas baseadas em funções elementares. “Era uma fatia fina de expressões possíveis”, disse ele. A rede neural não foi testada em funções mais complicadas, frequentemente usadas em física e finanças, como funções de erro ou funções de Bessel. (O grupo do Facebook disse que poderia ser, em versões futuras, com modificações muito simples.)
E Frédéric Gibou, matemático da Universidade da Califórnia, Santa Barbara, que investigou maneiras de usar redes neurais para resolver equações diferenciais parciais, não estava convencido de que a rede neural do grupo no Facebook fosse infalível. “Você precisa ter certeza de que funcionará o tempo todo, e não apenas de alguns problemas escolhidos”, disse ele, “e esse não é o caso aqui”. Outros críticos observaram que a rede neural do grupo no Facebook realmente não entende a matemática; é mais um adivinho excepcional.
Ainda assim, eles concordam que a nova abordagem será útil. Germundsson e Gibou acreditam que as redes neurais terão um lugar na mesa para os solucionadores de matemática simbólicos da próxima geração – será apenas uma mesa grande. “Acho que será uma das muitas ferramentas”, disse Germundsson.
Além de resolver esse problema específico da matemática simbólica, o trabalho do grupo no Facebook é uma prova encorajadora de princípios e do poder desse tipo de abordagem. “Os matemáticos em geral ficarão muito impressionados se essas técnicas lhes permitirem resolver problemas que as pessoas não podiam resolver antes”, disse Anders Hansen, matemático da Universidade de Cambridge.
Outra direção possível para a rede neural explorar é o desenvolvimento de geradores de teoremas automatizados. Os matemáticos estão cada vez mais investigando maneiras de usar a IA para gerar novos teoremas e provas, embora “o estado da arte não tenha feito muito progresso”, disse Lample. “É algo que estamos vendo”.
Charton descreve pelo menos duas maneiras pelas quais sua abordagem poderia levar os descobridores do teorema da IA para frente. Primeiro, poderia atuar como uma espécie de assistente de matemático, oferecendo assistência nos problemas existentes, identificando padrões em conjecturas conhecidas. Segundo, a máquina poderia gerar uma lista de resultados potencialmente prováveis que os matemáticos perderam. “Acreditamos que, se você puder fazer integração, poderá fazer provas”, disse ele.
Oferecer assistência para provas pode ser o aplicativo matador, mesmo além do que a equipe do Facebook descreveu. Uma maneira comum de refutar um teorema é criar um contra-exemplo que mostre que ele não pode aguentar. E é uma tarefa para a qual esses tipos de redes neurais podem um dia ser adequados: encontrar uma chave inesperada para jogar na máquina.
Outro problema não resolvido, em que essa abordagem se mostra promissora, é um dos aspectos mais perturbadores das redes neurais: ninguém realmente entende como elas funcionam. Os bits de treinamento entram em uma extremidade e os bits de previsão emergem da outra, mas o que acontece no meio – o processo exato que transforma as redes neurais em bons adivinhos – continua sendo uma questão crítica em aberto.
A matemática simbólica, por outro lado, é decididamente menos misteriosa. “Nós sabemos como a matemática funciona”, disse Charton. “Usando problemas matemáticos específicos como teste para ver onde as máquinas são bem-sucedidas e onde falham, podemos aprender como as redes neurais funcionam”.
Em breve, ele e Lample planejam alimentar expressões matemáticas em suas redes e rastrear a maneira como o programa responde a pequenas mudanças nas expressões. Mapear como as mudanças no gatilho de entrada muda na saída pode ajudar a expor como as redes neurais operam.
Zaremba vê esse tipo de entendimento como um possível passo para ensinar as redes neurais a raciocinar e a realmente entender as perguntas que estão respondendo. “É fácil em matemática mover a agulha e ver o quão bem [a rede neural] funciona se as expressões estão se tornando diferentes. Podemos realmente aprender o raciocínio, em vez de apenas a resposta ?, disse ele. “Os resultados seriam bastante poderosos.”
Publicado em 24/05/2020 11h34
Artigo original:
Estudo original:
Achou importante? Compartilhe!
Assine nossa newsletter e fique informado sobre Astrofísica, Biofísica, Geofísica e outras áreas. Preencha seu e-mail no espaço abaixo e clique em “OK”:




